Skip to main content

CS4246 Cheatsheet

Problem Specification​

  • Initial State
  • Possible Actions Action(s)
  • Transition Model Result(s,a)
  • Goal Test
  • Path Cost c(s,a,s')
  • Admissible Heuristic: Never overestimate cost to goal
  • Consistent / Monotonic: Straight path (to goal) always shorter than a curved path. h(n)≤c(n,a,n′)+h(n′)h(n) \leq c(n,a,n')+h(n')
  • Factored Representation: State representeed as SAT
  • Fluents: state variables in said representation

STRIPS​

  • Problem spec: Initial State, Actions, Result, Goal
    • Action: Action(params),
      • Precond: Descript
      • Effect: Descript
        • Negation (Delete list), otherwise Add List
    • Goal: Partial state, must be fulfilled
  • State: +ve literals ANDed together with no unknown variables or functions.
    • Negation not allowed (use literals that are negative)
    • If literal not specified in state, it is false (database semantics)
  • Search:
    • Forward: wk 1 39/65
    • Backward: wk 1 40/65
      • Relevant-state search:
        • Actions are relevant when:
          • Action doesn't negate a predicate in the current goal
          • Action unifies a predicate in the current goal
        • Add the preconditions of the action to current goal descript
    • Heuristics:
      • Ignore preconditions
      • Ignore delete lists
      • Assume subgoal independence, decompose problem
  • Turning into SAT problem
    • Complete the initial state by adding negations to omitted ground literals
    • Complete the goal by taking every possible grounded combination of the goal and ORing them together.
      • e.g. (On(A,A)T)∨(On(A,B)T)∨(On(A,A)^T) \vee (On(A,B)^T) \vee ...
  • Axioms
    • successor-state: Ft+1<=>ActionCausesFt∨(Ft∧¬ActionCausesNotFt)F^{t+1} <=> ActionCausesF^t \vee (F^t \wedge \neg ActionCausesNotF^t)
      • Solves Frame problem (most actions don't change fluents) 60/65
    • Pre-condition: Action taken at time => Precondition was true
    • Action Exclusion: both actions cannot be taken at same time step.
      • Not (Action1 at t) v Not (Action2 at v)

Utility Theory​

  • Axiomatic approach, assume agent has consistent preferences for outcomes (GT >, LT <, EQ ~). Represented as U(Outcome).
    • Utility can be preserved with monotonically increasing transformation.
  • Axioms
    • Orderability / Completeness: For any 2 outcomes, only 1 preference (agent prefers one, or both equal)
    • Transitivity: (A > B) /\ (B > C) => (A > C). Otherwise irrational
    • Continuity: If 3 outcomes: A > B > C where B is sandwiched. Then there must be a p where agent always get B, then A with probability p or C with probability (1 - p).
  • Lotteries: [p1, O1; p2, O2...] Probability p1 for outcome O1 etc
    • Susbstitutability: If A ~ B, then they can be swapped within a lottery
    • Monotonicity: If A > B, then agent must prefer A.
    • Decomposibility: 16/52 Chained lotteries can be reduced to simpler ones
  • Expectations:
    • Expected U(outcome): All probabilities x outcomes
    • Principle of Maximum Expected Utility (MEU)
      • Rational agents must maximize expected utility
    • Expected Monetary Value (EMV): wk1, 28/52
      • Risk-neutral: montonically increasing, line up
      • Risk-averse: Log of money amount.
      • Risk-seeking: U(L) is more than the straight line later on
      • Certainty Equivalent: Value agent will accept in lieu of a lottery
      • Risk Premium: EMV - certainty equiv
    • Normative theory: how agents should act
    • Descriptive theory: how they actually act
      • Irrationalities: Ambiguity aversion, framing effect, anchoring effect (35/52)
    • Optimizer's curse: 36/52
    • Bayesian and Decision networks 40/52
      • Given observed outcomes, calculate probability of affected outcomes
      • Chain rule
      • calculate expected outcome value based on these probabilities
    • Value of Perfect Information VPI
      • Given this new information, calculate new expected outcome
        • Split into cases (See 47/52)
          • Pr(info success) x Pr(success)
          • Pr(info fail) x Pr(fail)
        • VPI = new outcome - old outcome
      • Non-negative expected value
      • Not additive with other VPIs

MDP​

Principle of Optimality: A value of a state is its reward + best future rewards from state. 20/54

Online Search 39/54​

  • Handling curse of dimensionality with MDPs
    • Imagine it as a tree
    • Nodes: values , Edges: transitions
      • Tree size: ∣Actions∣D∣States∣D|Actions|^D |States|^D
  • Sparse Sampling: Don't check future for some states
  • Rollout: Simulate many trajectories from a state to estimate action with best returns
  • Monte Carlo Tree Search: 43/54
    • Selection: Dig down the tree until depth reached or node not simulated yet
      • GLIE. Explore first, then become more greedy (Decrease epsilon as time goes on).
    • Expansion: If state not terminal, Create child nodes from this state.
    • Simulation: Choose one of the child nodes,C, and do random rollout.
    • Backpropagation: Propagate the reesult of the rollout to update node values from C to root.
  • Upper Confidence Tree (UCT) 48/54
    • A strategy for selecting a node for MCTS
    • πUCT(n)=arg⁡max⁡a(Q^(n,a)+cln⁡(N(n))N(n,a))\pi_{U C T}(n)=\arg \max _{a}\left(\hat{Q}(n, a)+c \sqrt{\frac{\ln (N(n))}{N(n, a)}}\right)
      • Choose action that optimizes (current estimate + exploration * sqrt(ln(times node visited) / ln(times node visited and took action a))
      • Balance expected value and exploration

Bellman Eqn 21/54​

  • Evaluate policy using dynamic programming

  • Value Evaluation: Init V = 0

  • R(s)R(s): V(s)=R(s)+γ max⁡(E[V(s′)])V(s) = R(s) + γ\ \max (E[V(s')])

    • max⁡(E[V(s′)])=besta(E[V(s,a)])\max (E[V(s')]) = best_a (E[V(s,a)])
    • E[V(s,a)]=∑s′T(s,a,s′)V(s′)E[V(s,a)] = \sum_{s'} T(s,a,s')V(s')
    • V(s)=R(s)+γmax⁡∀a(∑∀s′T(s,a,s′)V(s′))V(s) = R(s) + γ \max_{\forall a}( \sum_{\forall s'} T(s,a,s')V(s'))

  • R(s,a)R(s,a): V(s)=max⁡a∈A[R(s,a)+γE[V(s,a)]]V(s) = \max_{a\in A}[R(s,a) + \gamma E[V(s,a)]]

  • R(s,a,s′)R(s,a,s'): V(s)=max⁡a∈A[∑s′∈ST(s,a,s′)[R(s,a,s′)+γV(s′)]]V(s) = \max_{a\in A}[ \sum_{s'\in S} T(s,a,s')[R(s,a,s') + \gamma V(s')]]

    • (s): state, (s,a): action, (s,a,s'): transition

  • Value Iteration: Given model (R, A, T(s,a,s')), recurse bellman until all V(s)V(s) converge

  • Policy Iteration: Init V = 0, π\pi = random

    • Evaluate Vt+1V_{t+1} based on π\pi, not max (using bellman)
    • Update π\pi if V for any action π(s)\pi(s) < max⁡(E[V(s′)])\max (E[V(s')])
    • Stop when π\pi no change / horizon reached

  • Prediction: Evaluate a given policy, Control: Find optimal policy

  • Model-Based, Adaptive Dynamic Programming Agent: Iteratively given observations, construct R and T(s,a,s'):

    • R: = observed R(s). In addition, U(s) = R(s) when a new R(s) is observed
    • T(s,a,s'): (times transition observed) / (times action at state)
      • these variables are tracked with a table
    • Prediction: Update U using Policy-Evaluation after each observation
    • Control: Update U using Policy-Iteration after each observation

  • ϵ\epsilon-greedy: action = (1-e)(best) and (e)(random)

  • Greedy in the Limit of Infinite Exploration (GLIE), ϵ=1/t\epsilon=1/t

  • Monte Carlo Learning (Direct Utility Estimation): Vπ(s)=E[∑V^{\pi}(s) = E[\sum of rewards from s to end]

    • Gi(s)G_i(s) = ∑\sum of rewards from s to end
      • i-th episode, k episodes thus far
    • Concept: Vk(s)+=V_k(s) += [(New Info) - (Current Estimate)]
      • New Info = Target, Difference = Error
    • Vk(s)V_k(s) equals (1k∑i=1kGi(s))(\frac{1}{k}\sum_{i=1}^{k}G_i(s)) equals (Vk−1(s)+1k(Gk(s)−Vk−1(s)))(V_{k-1}(s) + \frac{1}{k}(G_k(s) - V_{k-1}(s)))
    • Monte Carlo Target: Gk(s)G_k(s)
    • Monte Carlo Error (converges to 0 when k = ∞\infty): (Gk(s)−Vk−1(s))(G_k(s) - V_{k-1}(s))
    • Prediction: Calculating V(s) is enough
    • Control: Calculate Vk(s,a)=(1k∑i=1kGi(s,a))V_k(s,a)=(\frac{1}{k}\sum_{i=1}^{k}G_i(s,a)), then update π\pi by π(s)=max⁡V(s,a)\pi(s) = \max V(s,a)

  • Temporal Difference Learning (TD(0)): Same as MC Learning but estimate V(s)V(s) with every step in the episode instead.

    • Change the target:
    • Vk[j+1](s)=Vk[j](s)+α(target−Vk[j](s))V_{k[j+1]}(s) = V_{k[j]}(s) + \alpha(target - V_{k[j]}(s))
    • $ = V{k[j+1]}(s) = V{k[j]}(s) + \alpha(R{k[j+1]}(s) + \gamma V{k[j]}(s') - V_{k[j]}(s))$
      • k episodes thus far, j-th step in the kth episode
    • TD Target: Rk[j+1](s)+γVk[j](s′)R_{k[j+1]}(s) + \gamma V_{k[j]}(s')
    • Converges faster but biased
    • SARSA: TD(0) using 1 π\pi for generating data and training(on-policy)
      • State-action-reward-state-action: algo for learning MDP
      • Future value estimate by action taken by π\pi
      • Target: R(s,a)+γV(s′,π(s′))R(s,a) + \gamma V(s',\pi(s'))
      • on-policy converges if ϵ\epsilon-greedy
    • Q-Learning: TD(0) using 2 π\pi: 1 for generating data, 1 training (off-policy)
      • Future value estimate by best action based on current estimates
      • Target: R(s,a)+γmax⁡a∈A(s′)V(s′,abest)R(s,a) + \gamma \max_{a\in A(s')} V(s',a_{best})
      • off-policy converges if α\alpha decays and all transitions taken infinitely times

  • n-step TD (TD(n)): Somewhere between TD & MC: Change target to combine future steps in 1 update

    • 0-step (Gt(0)G_t^{(0)}): TD target = R(s)R(s)
    • 1-step (Gt(1)G_t^{(1)}): TD target = R(s)+γV(s′)R(s) + \gamma V(s')
    • 2-step (Gt(2)G_t^{(2)}): TD target = R(s)+γR(s′)+γ2V(s′′)R(s) + \gamma R(s') + \gamma^2 V(s'')

  • TD(λ\lambda): n = ∞\infty, λ\lambda = 0 to 1, weight and normalize by geometric progression

    • λ0Gt(1)+λ1Gt(2)+...+λ∞−1Gt(∞)\lambda^0 G_t^{(1)} + \lambda^1 G_t^{(2)} + ... + \lambda^{\infty-1} G_t^{(\infty)}
      • Gt(n)G_t^{(n)}: New observed V(s) given n-step estimation
      • Conceptually, All GtG_t are estimations of the same thing, hence the eqn = ∑n=0∞λnGt\sum_{n=0}^{\infty}\lambda^n G_t
      • Using Geom Progression: ∑n=0∞λn=11−λ\sum_{n=0}^{\infty}\lambda^n = \frac{1}{1-\lambda}
    • Hence Gtλ=(1−λ)∑n=0∞λn−1Gt(n)G^\lambda_t = (1-\lambda)\sum_{n=0}^{\infty}\lambda^{n-1} G_t^{(n)}
    • Computation:
      • Eligibility trace ee: track how "fresh" each state is by frequency and last visit
        • Init = 0
        • Types:
          • Accumulating ee: += 1 if state visited at step
          • Replacing ee: = 1 if state visited at step
        • "Decaying Effect": With every timestep, e=λγee = \lambda\gamma e
    • Using eligibility traces, ∀s\forall s and timestep, update V(s). The TD error is weighted by each state's own eligibility trace.
    • ∀\forall timestep, update all eligibility traces:
      • eligibility *= lambda * gamma
      • eligibility[state] += 1.0
    • Then get the TD error for the current timestep: td_error = reward + gamma * state_values[new_state] - state_values[state]
    • Then finally update U(s) for all states: state_values = state_values + alpha * td_error * eligibility

Function Approximation​

  • State space too large, approximate V(s)V(s) with a linear function that takes in a vector of params θ\theta:
  • V^θ(s)=θ1f1(s)+θ2f2(s)+⋯+θnfn(s)\hat{V}_{\theta}(s)=\theta_{1} f_{1}(s)+\theta_{2} f_{2}(s)+\cdots+\theta_{n} f_{n}(s)
    • Multi-variate s: V^θ(x,y)=θ0+θ1x+θ2y\hat{V}_{\theta}(x,y)=\theta_{0} + \theta_{1}x+\theta_{2} y, where s=(x,y)
    • V^(s,a)\hat{V}(s, a): Can approximate by:
      • Keep a constant, then estimate using 1 linear fx per s
      • Use a single linear fx that accepts s and a as params
  • Supervised Learning
    • Learn using initial training sample set
    • Do least squares estimation to fit params
      • e.g. given linear function V^θ(x,y)=θ0+θ1x+θ2y\hat{V}_{\theta}(x,y)=\theta_{0} + \theta_{1}x+\theta_{2} y
      • you have a set of samples {((x1,y1,u1),(x2,y2,u2),...,(xn,yn,un)}\{((x_1,y_1,u_1),(x_2,y_2,u_2),...,(x_n,y_n,u_n)\} where V is value of the linear function and x and y are the function input, do linear regression to solve
  • Online Learning
    • Use gradient descent to minimize Error(s) (MC Error, TD Error etc) by modifying params θ\theta on every observation
    • Error(s) = 12[\frac{1}{2}[ (approximated_V(s)) - (observed_V(s))]2]^2
      • "approximated_V(s)" is V^θ(s)\hat{V}_{\theta}(s)
      • θi=θi+αδd(s)δθi=θi+α(\theta_i = \theta_i + \alpha \frac{\delta d(s)}{\delta\theta_i} =\theta_{i}+\alpha( observed_V(s) - approximated_V(s) )∂V^θ(s)∂θi) \frac{\partial \hat{V}_{\theta}(s)}{\partial \theta_{i}}
        • ∂V^θ(s)∂θi\frac{\partial \hat{V}_{\theta}(s)}{\partial \theta_{i}}: differentiate linear function w.r.t. θi\theta_i
      • You can swap out the error portion in the θ\theta assignment above with any of these:
        • Monte Carlo Error: (approximated_V(s)) - (observed_V(s))
        • Semi-gradient methods (target biased as it depends on θ\theta):
        • TD Error: θi←θi+α[R(s)+γV^θ(s′)−V^θ(s)]∂V^θ(s)∂θi\theta_{i} \leftarrow \theta_{i}+\alpha\left[R(s)+\gamma \hat{V}_{\theta}\left(s^{\prime}\right)-\hat{V}_{\theta}(s)\right] \frac{\partial \hat{V}_{\theta}(s)}{\partial \theta_{i}}
        • Q-Learning "Error": θi←θi+α[R(s)+γmax⁡a′V^θ(s′,a′)−V^θ(s,a)]∂V^θ(s,a)∂θi\theta_{i} \leftarrow \theta_{i}+\alpha\left[R(s)+\gamma \max _{a^{\prime}} \hat{V}_{\theta}\left(s^{\prime}, a^{\prime}\right)-\hat{V}_{\theta}(s, a)\right] \frac{\partial \hat{V}_{\theta}(s, a)}{\partial \theta_{i}}
  • Deadly Triad: Sources of instability
    1. Function Approximation
    2. Bootstrapping: Use current estimates as targets, e.g. TD Rather than complete returns, e.g. MC
    3. Off-policy: Training on transitions other than that produced by the target policy.

Deep Q-Learning: Q-learning with non-linear function approximation​

  • Use experience replay with fixed Q-targets to make inputs less correlated & reduce instability
  • The procedure below uses double Q-learning
  • Procedure:
  1. Take ϵ-greedy action ata_t using approximated policy from main policy_NN
  2. Store observed transition (st,at,rt+1,st+1)(s_t,a_t,r_{t+1},s_{t+1}) in a round-robin buffer
  3. Repeat until tmaxt_{max} transitions, then loop stepstrainingsteps_{training} times:
    1. Sample random mini-batch of transitions from buffer. Do the following as a batch:
    2. Compute VmainNN(s)V^{mainNN}(s) based on actions policy_NN took to produce the transition
    3. Compute VtargetNN(s)=R(s)+γ(max⁡VtargetNN(s′)V^{targetNN}(s) = R(s) + \gamma(\max V^{targetNN}(s')
      • Compute max⁡VtargetNN(s′)\max V^{target_NN}(s') by ∀s′,E[VtargetNN(s′,a′)]\forall s', E[V^{target_NN}(s',a')]
    4. Compute Huber loss between VmainNN(s,a)V^{mainNN}(s,a) and VtargetNN(s)V^{targetNN}(s)
    5. Gradient step on loss
  4. Increment episode count
  5. Set target_NN's params to main_NN's params after every C episodes
  6. Reset environment, update ϵ\epsilon and repeat from step 1

POMDP​

  • Updating belief' given (b, a, e)
  • b′(scurr)=normalized Pr(e∣scurr)∗E[(sprev,a,scurr)]b'(s_{curr})=normalized\ Pr(e | s_{curr}) * E[(s_{prev}, a, s_{curr})]
    • E[(sprev,a,scurr)]=Pr(scurr∣sprev,a)∗b(sprev)E[(s_{prev}, a, s_{curr})] = Pr(s_{curr} | s_{prev},a) * b(s_{prev})
  1. Set initial belief (set of probabilities of being in each state)
  2. Do action: ∀\forall next_state, ∑\sum all Pr(you were in prev_state) x Pr(transit)
  3. Use evidence: ∀\forall state, x Pr(evidence seen at state)
  4. Normalize s.t. ∑\sum all state beliefs = 1
  • Value (α(sstart)\alpha(s_{start})) of plan a1,...,ana_1,...,a_n with n steps
    • α[a1,...,an](sstart)=R(sstart)+γ(E[α[a2,...,an](snext)])\alpha_{[a_1,...,a_{n}]}(s_{start})=R(s_{start}) + \gamma(E[\alpha_{[a_2,...,a_{n}]}(s_{next})])
      • Recursively "unpack" future rewards as necessary
    • Evaluate E[value] after executing plan from sstarts_{start}
    • Plan: Pre-planned sequence of steps
    • Optimal Plan:
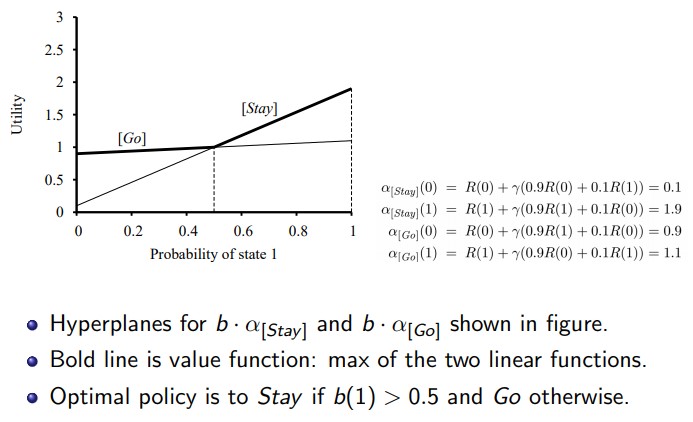
      • x-axis: Pr(sstart==ss_{start} == s) (0-1), y-axis: value αp(s)\alpha_p(s))
      • Plot: All possible values of plans w.r.t. Pr(s) (α[∀permutations](s)\alpha_{[\forall permutations]}(s)). Each plan is a line formed by 2 points:
        • Point 1 at x-axis 0: α[a1,...,an](not sstart)\alpha_{[a_1,...,a_{n}]}(not\ s_{start})
        • Point 2 at x-axis 1: α[a1,...,an](sstart)\alpha_{[a_1,...,a_{n}]}(s_{start})
      • Optimal: Switch between plans that offers highest αp(s)\alpha_p(s) given regions of Pr(sstart==ss_{start} == s)
      • POMDP Value Iteration: Keep calculating plans while removing dominated plans. If no change after awhile, then return set of dominating plans.